Diseño de reactores. Parte 24. Lodos activados. Efecto de la temperatura.

Diseño de reactores. Parte 24. Modelación del proceso de lodos activados. Efecto de la temperatura.

Categoría: 2. Ciencia y tecnología.

Este ejercicio está basado en ejercicios del capítulo 6 de Martínez y Rodríguez (2005).

Ejercicio VI-2

Con base en el efecto de la temperatura en la velocidad específica de crecimiento (ecuación VI-15), introduzca el efecto de la temperatura y desarrollo el programa para evaluar este efecto en un sistema de tratamiento de agua residual doméstica mediante lodos activados utilizando esas mismas ecuaciones y los parámetros correspondientes.

Se debe resolver el sistema de ecuaciones siguiente:

ds/dt=(Qf*Sf)/V-(Qf*S)/V-(mumax/Y)*(S/(Ks+S))*(Co2/(KOH+Co2))*X+kd*(1-fn)*X

dX/dt=(Qf*X)/V+mumax*(S/(Ks+S))*(Co2/(KOH+Co2))*X-kd*X

dCo2/dt=-(Qo*Co2)/V-(mumax/Yo2)*(S/(Ks+S))*(Co2/(KOH+Co2))*X+kla*(Cosat-Co2)

KOH= coeficiente de saturación de oxígeno (mg/L)

Yo2= coeficiente de rendimiento de O2 (mg biomasa generada/mg de O2 consumido)

El código en MATLAB se escribió en dos programas, lodosactivadostemp.m y lodosactivadostemprun.m. En el primero de ellos se planteó el sistema de ecuaciones y en el segundo se colocaron las instrucciones para ejecutar la solución y generar los gráficos (Figuras 13 a 16). En el programa lodosactivadostemprun.m se utilizó el signo % de manera que se generaba el gráfico para un parámetro a la vez. El código de estos dos programas se muestra a continuación:

% lodosactivadostemp

function dy=lodosactivadostemp(t,y)

Sf=310;

Tw=16;

if t<1460

    Tw=16;

elseif t<2920

    Tw=19;

elseif t<4380

    Tw=23;

elseif t<5840

    Tw=25;

elseif t<7300

    Tw=28;

elseif t<8760

    Tw=30;

end

% coeficientes de la ecuacion VI-15

a1=0.1373;

b1=22.91;

c1=17.59;

% ecuacion VI-15

mumax=a1*exp(-((Tw-b1)/c1)^2);

Y=0.71;

fn=0.1;     % fraccion de inertes en los SSV

Ks=35;

kd=0.002*1.05^(Tw-20);  % ecuacion VI-19

Yo=2.03;

Koh=0.2;

O2o=0.3;

kla20=6.0;

kla=kla20*1.02^(Tw-20);     % ecuacion III-10a

beta=0.985;

O2sat=((0.0035*Tw^2)-0.3355*Tw+14.465)*beta;    % ecuacion VI-21

Qf=120;

Qr=15;

Qw=5;

V=500;

Vs=100;

% sistema de ecuaciones

dy=zeros(4,1);

% ecuacion de comportamiento de sustrato en el reactor

dy(1)=(Qf/V)*Sf-((Qf+Qr)/V)*y(1)-((mumax/Y)*y(1)*y(2)/(Ks+y(1)))*((y(4)/(Koh+y(4))))+(1-fn)*y(2)*kd;

% ecuacion de comportamiento de SSV en el reactor

dy(2)=(Qr/V)*y(3)-((Qf+Qr)/V)*y(2)+((mumax*y(1)*y(2))/(Ks+y(1)))*(y(4)/(Koh+y(4)))-kd*y(2);

% ecuacion de comportamiento de SSv en el sedimentador

dy(3)=((Qf+Qr)/Vs)*y(2)-((Qr+Qw)/Vs)*y(3);

% ecuacion de comportamiento de oxigeno en el reactor

dy(4)=kla*(O2sat-y(4))+(Qf/V)*O2o-((Qf+Qr)/V)*y(4)-(((1/Yo)*mumax*y(1)*y(2))/(Ks+y(1)))*(y(4)/(Koh+y(4)));

% lodosactivadostemprun

[t,y]=ode45('lodosactivadostemp',[0 8760],[250 120 1000 4]);

% grafico para DQO

%plot(t,y(:,1),'k-')

%xlabel('tiempo (h)')

%ylabel('DQO (mg/L)')

%title('comportamiento dinamico de la DQO en diferentes temperaturas')

%text(730,90,'16°C')

%text(2190,90,'19°C')

%text(3650,90,'23°C')

%text(5110,90,'25°C')

%text(6570,90,'28°C')

%text(8030,90,'30°C')

% grafico para SSV

%plot(t,y(:,2),'k-')

%xlabel('tiempo (h)')

%ylabel('SSV (mg/L)')

%title('comportamiento dinamico de SSV en el reactor a diferentes temperaturas')

%text(730,675,'16°C')

%text(2190,675,'19°C')

%text(3650,675,'23°C')

%text(5110,675,'25°C')

%text(6570,675,'28°C')

%text(8030,675,'30°C')

% grafico para SSVS

%plot(t,y(:,3),'k-')

%xlabel('tiempo (h)')

%ylabel('SSVS (mmg/L)')

%title('comportamiento dinamico de SSVS en el sedimentador a diferentes temperaturas')

%text(730,1500,'16°C')

%text(2190,1500,'19°C')

%text(3650,1500,'23°C')

%text(5110,1500,'25°C')

%text(6570,1500,'28°C')

%text(8030,1500,'30°C')

%axis([0 9000 500 5000])

% grafico para OD

plot(t,y(:,4),'k-')

xlabel('tiempo (h)')

ylabel('OD (mg/L)')

title('comportamiento dinamico de OD en el reactor a diferentes temperaturas')

text(730,7.5,'16°C')

text(2190,7.5,'19°C')

text(3650,7.5,'23°C')

text(5110,7.5,'25°C')

text(6570,7.5,'28°C')

text(8030,7.5,'30°C')

Figura 13. Gráfico del comportamiento dinámico de la DQO en el efluente a diferentes temperaturas.

Figura 14. Gráfico del comportamiento dinámico de SSV dentro del reactor a diferentes temperaturas.

Figura 15. Gráfico del comportamiento dinámico de la concentración de SSV en el fondo del sedimentador a diferentes temperaturas.

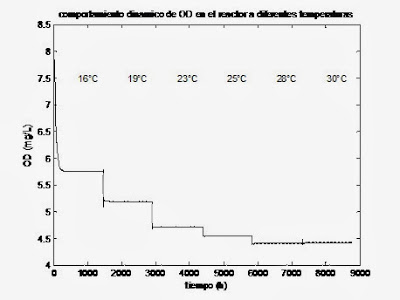
Figura 16. Gráfico del comportamiento dinámico de la concentración de oxígeno disuelto dentro del reactor a diferentes temperaturas.

Bibliografía

Martínez D., Sergio A. y Miriam G. Rodríguez R.2005. Tratamiento de aguas residuales con MATLAB. Editorial Reverté. Universidad Autónoma Metropolitana. México, DF, México.