Python básico para estadística.
Categoría: 2. Ciencia y tecnología.
En esta entrada se presenta un ejercicio básico de estadística utilizando como herramienta el lenguaje de programación Python.
En un principio se trata de elaborar un programa mínimo en Python que pueda correrse sin dificultades. A continuación se agregan funciones para obtener un código más complejo.
Si encuentras de interés esta información, tal vez te sea útil visitar una entrada donde resuelvo problemas parecidos utilizando MATLAB: Análisis de varianza para un blog.
Si encuentras de interés esta información, tal vez te sea útil visitar una entrada donde resuelvo problemas parecidos utilizando MATLAB: Análisis de varianza para un blog.
Se puede trabajar en la ventana de Python para realizar cálculos relativamente simples. Cálculos repetitivos se pueden manejar con funciones, que están activas solamente durante el tiempo que dura la sesión. Puede realizar por ejemplo los siguientes cálculos con números binarios:
>>> y=0b0001
>>> for i in range(1,5):
... y=y<<1
... print y
...
2
4
8
16
>>>
El primer paso es entonces crear un archivo de texto con el nombre estadistica_1.txt. Selecciona un destino donde puedas guardar estos archivos, por ejemplo, una memoria USB en la unidad E:(E:/estadistica_codigo.txt). En esta unidad también es recomendable crear una carpeta llamada python donde guardar los archivos con extensión .py: E:/python/.
También vas a utilizar el directorio raíz de la unidad E: para guardar los archivos de salida.
Algunas instrucciones previas para explicar lo que vamos haciendo:
- En Python se coloca un signo hash (#) para iniciar un comentario.
- Se deben llamar las librerías necesarias que contengan las funciones que ocupamos en el código. Esto se hace al inicio, después del nombre del programa y los créditos.
- Se pueden crear funciones que se ejecutan desde la ventana principal de Python.
- La indentación es muy importante para que se ejecute el código.
- La instrucción print despliega los valores de salida en la ventana de sistema.
- En el manejo de archivos no olvides utilizar las instrucciones de apertura, f=open('file.txt',"w") y de cierre, f.close().
Ejercicio en la ventana principal de Python. Después de la primera instrucción, def writefile(): se debe pulsar la tecla tab al inicio de la siguentes instrucciones; las instrucciones que estén dentro del ciclo for necesitan dos tab de indentación. Escribir una función que envía datos a un archivo de salida:
>>> def writefile():
... f=open("E:/myfile.txt","a")
... f.write("\n")
... for i in range(-10,10):
... i=i**3
... print i,"\t"
... v=str(i) # Convierte int a cadena
... f.write(v)
... f.write("\t")
... f.close()
...
Es importante mencionar algunos modos en que puede abrirse un archivo para escribir datos.
Escribir datos en archivo de salida:
- Función: open() # deveulve un objeto archivo
- open(nombre_de_archivo, modo)
modo acción
'r' Lectura
'w' Escritura
'a' Abre archivo para agregar información.
El dato se agrega automáticamente al final.
'r+' Abre archivo tanto para lectura como para escritura.
Ahora vas a preparar el mismo programa en un archivo con extensión .py para poderlo ejecutar de manera repetitiva sin necesidad de escribirlo cada vez, como lo haces en la ventana principal de Python. Lo primero que destaca es que se elimina la linea con el nombre de la función - def writefile(): - y también se agrega la instrucción raw_input() al final del código.
f=open("E:/myfile.txt","a")
f.write("\n")
for i in range(-10,10):
i=i**3
print i,"\t"
v=str(i) # Convierte int a cadena
f.write(v)
f.write("\t")
f.close()
raw_input()
Este código lo capturas en un archivo de texto: E:/vector_Codigo.txt; y guardas. Ahora seleccionas [Archivo] [Guardar como], te desplazas a la carpeta E:/python/ y guardas el archivo como E:/python/vector.py. Recuerda colocar las indentaciones (un tab) en la cinco instrucciones dentro del ciclo for.
Es importante que lleve la extensión .py, de lo contrario no podrá ejecutarse tu código. La máquina donde se corre el programa debe tener instalado Python 2.7. En el explorador de archivos seleccionas el archivo vector.py y das [Enter]. Aparece una ventana de sistema desplegando los resultados. Das [Enter] para cerrar esta ventana de salida y te desplazas en el explorador de archivos hasta E: Ahí seleccionas el archivo myfile.txt y das [Enter]. Entonces puedes ver los resultados de tu primer programa.
Nota que para este programa sólo utilizas funciones instaladas en la librería principal. Por eso no se incluyeron bibliotecas en el inicio del código.
****************************** *************************************
En el siguiente ejemplo se parte de tres conjuntos de datos, vectores dataset_1, dataset_2 y dataset_3, y se realizan los cálculos de la prueba de Wilcoxon y la prueba de Kruskal-Wallis.
La prueba de Wilcoxon se utiliza para poner a prueba la hipótesis nula Ho: mu1=mu2, contra la hipótesis alternativa H1: mu1 != mu2. Si el valor calculado para la prueba, w_calculada, es menor o igual que w_alfa, la hipótesis nula se rechaza (en este caso != se lee "no igual o diferente a").
Esta prueba solo se utiliza para la comparación de datos en pares. En el ejemplo, la prueba se realiza sobre los conjuntos de datos dataset_1 vs dataset_2 y sobre dataset_2 vs dataset_3.
Puedes ver el código de Programa1 al fina de esta página. La figura siguiente muestra la ventana de salida.
Salida de Programa1.
En la comparación de los conjuntos dataset_1 vs dataset_2 la prueba genera los siguientes resultados: 8.5, 0.05. El primero corresponde a w+ y el segundo a w-. Como el menor de estos valores es menor que w_alfa se rechaza Ho: mu1=mu2 para dataset_1 vs dataset_2. El siguiente resultado muestra 0.0, 0.01, se rechaza Ho: mu1=mu2 para dataset_2 vs dataset_3.
La prueba de Kruskal-Wallis se utiliza para comparar los promedios de dos o más conjuntos de datos, que pueden ser los resultados de tratamientos diferentes en un experimento. Cuando se presume que los datos no muestran una distribución normal. El estadístico de prueba, H, se compara con el valor de Xi^2 con significancia alfa y a-1 grados de libertad. Donde a es el número de conjuntos de datos o tratamientos de donde provienen las muestras. Si el valor de H es mayor que Xi^2,alfa,a-1, Ho se rechaza. Se trata de probar Ho: mu1=mu2= ... =mu_n.
El resultado que muestra el programa despliega el valor de S^2 y de H. En el ejemplo S^2=22.5 y H=1.3e-5. Como el valor de X^2,0.05,2 es de 5.99, el estadístico de prueba cae dentro de la zona de rechazo de Ho. De manera que dataset_1 != dataset_2 != dataset_3.
La curtosis es un valor que indica la forma en que se distribuyen los datos alrededor de la media. Un valor elevado indica que los datos se concentran cerca de la media. En este ejemplo se tienen valores bajos para la curtosis. Esto se explica por la gran dispersión alrededor del promedio, como lo indican los valores altos de la varianza.
****************************** *************************************
En el ejemplo a continuación, se presenta el análisis de varianza para los tres conjuntos de datos que se utilizaron en el ejemplo anterior.
Puedes ver el código de Programa2 al fina de esta página. La salida del programa tiene el aspecto siguiente:
Salida de Programa2:
El resultado del análisis de varianza muestra que el valor del estadístico de prueba es F=204.1; el otro es el valor del estadístico p, que en este caso es p=5.01e-17. Para una prueba con significancia alfa=0.05 la hipótesis nula Ho: mu1=mu2=mu3 se rechaza. En este caso es claro por el elevado valor de F, marcadamente dentro de la zona de rechazo. El valor de p<<0.05 indica que el estadístico de prueba quedó bastante dentro de la zona de rechazo de Ho.
Debe recordarse que en esta prueba debe rechazarse Ho: tao_1=tao_2= ... tao_n=0, si f_obs > f_alfa_a-1_a(n-1).
El valor F con n-1 grados de libertad en el numerador y a(n-1) grados de libertad en el denominador y significancia alfa=0.05, que para este caso es F0.05,2,27=3.35, comparado con el valor f_obs=204.1 nos dice que se debe rechazar Ho.
****************************** *************************************
Ahora una función que crea un vector de nombre A y lo llena con valores generados aleatoriamente.
Puedes ver el código de Programa3 al fina de esta página. La salida del programa tiene el aspecto siguiente:
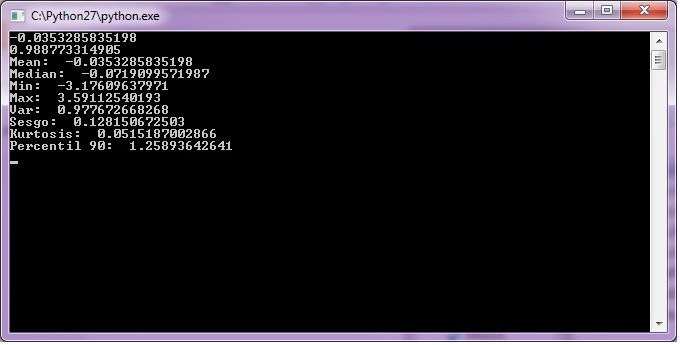
Salida Programa3.
Los valores de salida son diferentes cada vez que se corre el programa. De manera que nunca vas a obtener los mismos resultados que aparecen en esta imagen.
El programa genera un conjunto de 1000 valores con un generador de números aleatorios con distribución normal. En la salida se muestran los estadísticos que describen al conjunto. Aparece la media, mediana, mínimo, máximo, varianza, sesgo, curtosis y percentil 90.
El sesgo es un valor de la asimetría que se aplica a un histograma o a una distribución de probabilidad. Como la curtosis, es un valor que describe la simetría de un conjunto de datos alrededor del promedio. Su valor puede ser positivo, negativo, cero o inclusive una indefinición. Su interpretación no es muy directa, pero en una distribución unimodal un valor negativo del sesgo indica que hay una cola más alargada en el lado izquierdo de la función de densidad de probabilidad.
************************* ****************************
Conclusiones.
Los estadísticos que describen un conjunto de datos pueden calcularse de manera sencilla en python.
El análisis de varianza para hacer comparaciones entre las varianzas de varios conjuntos de datos para saber si provienen de poblaciones independientes, se puede hacer con python de manera rápida.
Una vez que se corren algunos ejercicios en python se puede experimentar con programas más complicados.
Visita la página web de python. Ahí puedes descargar python 2.7, por ahora la versión más reciente.
También puedes visitar la página web de SciPy, donde puedes descargar librerías: NumPy, SciPy, SymPy, MatPlotLib y Pandas.
Bibliografía.
Montgomery, Douglas C., and George C. Runger. 2003. Applied statistics and probability for engineers. Third edition. John Willey $ Sons Inc. United States of America.
Cárdenas Montes, Miguel. Estadística. Site: http://wwwae.ciemat.es/~cardenas/curso_MD/Estadistica.pdf
************************************ ******************************
************************************ ******************************
Código Programa1:
# Practica: Estadistica inferencia
# Se trabaja sobre los mismos datos que Estadistica basica
# Prueba de Kruskal-Wallis
# Prueba de Wilcoxon con signo
import scipy.stats
dataset_1=[326.4,324.9,316.3,302.8,317.0,325.4,311.9,322.4,312.1,322.2]
dataset_2=[299.0,301.9,309.4,316.9,304.8,314.2,305.3,308.9,312.5,308.1]
dataset_3=[264.8,275.9,259.0,270.6,266.7,261.8,266.1,268.4,266.2,267.4]
print 'dataset_1: ',dataset_1,'\n','Media: ',scipy.mean(dataset_1)
print 'dataset_2: ',dataset_2,'\n','Media: ',scipy.mean(dataset_2)
print 'dataset_3: ',dataset_3,'\n','Media: ',scipy.mean(dataset_3)
f=open('E:/Estadistica_Inferencia.txt','a')
f.write("Dataset_1: " + str(dataset_1) + '\n')
f.write("Media dataset_1: " + str(scipy.mean(dataset_1)) + '\n')
f.write("Dataset_2: " + str(dataset_2) + '\n')
f.write("Media dataset_2: " + str(scipy.mean(dataset_2)) + '\n')
f.write("Dataset_3: " + str(dataset_3) + '\n')
f.write("Media dataset_3: " + str(scipy.mean(dataset_3)) + '\n')
print 'dataset_1 Median: ',scipy.median(dataset_1)
f.write("Dataset_1 Median: " + str(scipy.median(dataset_1)) + '\n')
print 'dataset_2 Median: ',scipy.median(dataset_2)
f.write("Dataset_2 Median: " + str(scipy.median(dataset_2)) + '\n')
print 'dataset_3 Median: ',scipy.median(dataset_3)
f.write("Dataset_3 Median: " + str(scipy.median(dataset_3)) + '\n')
print 'dataset_1 Min: ',min(dataset_1)
f.write("Dataset_1 Min: " + str(min(dataset_1)) + '\n')
print 'dataset_2 Min: ',min(dataset_2)
f.write("Dataset_2 Min: " + str(min(dataset_2)) + '\n')
print 'dataset_3 Min: ',min(dataset_3)
f.write("Dataset_3 Min: " + str(min(dataset_3)) + '\n')
print 'dataset_1 Max: ',max(dataset_1)
f.write("Dataset_1 Max: " + str(max(dataset_1)) + '\n')
print 'dataset_2 Max: ',max(dataset_2)
f.write("Dataset_2 Max: " + str(max(dataset_2)) + '\n')
print 'dataset_3 Max: ',max(dataset_3)
f.write("Dataset_3 Max: " + str(max(dataset_3)) + '\n')
print 'dataset_1 Var: ',scipy.var(dataset_1)
f.write("Dataset_1 Var: " + str(scipy.var(dataset_1)) + '\n')
print 'dataset_2 Var: ',scipy.var(dataset_2)
f.write("Dataset_2 Var: " + str(scipy.var(dataset_2)) + '\n')
print 'dataset_3 Var: ',scipy.var(dataset_3)
f.write("Dataset_3 Var: " + str(scipy.var(dataset_3)) + '\n')
print 'dataset_1 Sesgo: ',scipy.stats.skew(dataset_1)
f.write("Dataset_1 Sesgo: " + str(scipy.stats.skew(dataset_1)) + '\n')
print 'dataset_2 Sesgo: ',scipy.stats.skew(dataset_2)
f.write("Dataset_2 Sesgo: " + str(scipy.stats.skew(dataset_2)) + '\n')
print 'dataset_3 Sesgo: ',scipy.stats.skew(dataset_3)
f.write("Dataset_3 Sesgo: " + str(scipy.stats.skew(dataset_3)) + '\n')
print 'dataset_1 Kurtosis: ',scipy.stats.kurtosis(dataset_1)
f.write("Dataset_1 Kurtosis: " + str(scipy.stats.kurtosis(dataset_1)) + '\n')
print 'dataset_2 Kurtosis: ',scipy.stats.kurtosis(dataset_2)
f.write("Dataset_2 Kurtosis: " + str(scipy.stats.kurtosis(dataset_2)) + '\n')
print 'dataset_3 Kurtosis: ',scipy.stats.kurtosis(dataset_3)
f.write("Dataset_3 Kurtosis: " + str(scipy.stats.kurtosis(dataset_3)) + '\n')
KW_test=scipy.stats.kruskal(scipy.array(dataset_1),scipy.array(dataset_2),scipy.array(dataset_3))
Wi_test_1vs2=scipy.stats.wilcoxon(dataset_1,dataset_2)
Wi_test_2vs3=scipy.stats.wilcoxon(dataset_2,dataset_3)
print 'Kruskal-Wallis test: ',KW_test
f.write("Kruskal-Wallis test: " + str(KW_test) + '\n')
f.write("Wilcoxon signed-rank test dataset_1 vs dataset_2: " + str(Wi_test_1vs2) + '\n')
f.write("Wilcoxon signed-rank test dataset_2 vs dataset_3: " + str(Wi_test_2vs3) + '\n')
print 'Wilcoxon signed-rank test dataset_1 vs dataset_2: ',Wi_test_1vs2
print 'Wilcoxon signed-rank test dataset_2 vs dataset_3: ',Wi_test_2vs3
f.write('\n')
f.close()
******************************* ****************************
Código Programa2:
# Practica: ANOVA
#
# print 'X= %5.3f' % X[i]
import numpy as np
import scipy.stats
import random
from numpy import array
from scipy.stats import kstest
dataset_1=[326.4,324.9,316.3,302.8,317.0,325.4,311.9,322.4,312.1,322.2]
dataset_2=[299.0,301.9,309.4,316.9,304.8,314.2,305.3,308.9,312.5,308.1]
dataset_3=[264.8,275.9,259.0,270.6,266.7,261.8,266.1,268.4,266.2,267.4]
f=open('E:/Estadistica_ANOVA.txt','a')
anova_ans=scipy.stats.f_oneway(dataset_1,dataset_2,dataset_3)
print 'ANOVA: ',anova_ans
f.write('ANOVA: ')
w=str(anova_ans)
f.write(w)
f.write("\n")
# ***
f.write('dataset_1: ')
v=str(dataset_1)
f.write(v)
f.write("\n")
f.write('dataset_2: ')
v=str(dataset_2)
f.write(v)
f.write("\n")
f.write('dataset_3: ')
v=str(dataset_3)
f.write(v)
f.write("\n")
# ***
v=scipy.mean(dataset_1)
print 'Mean dataset_1: ',v
w=str(v)
f.write('Mean dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.mean(dataset_2)
print 'Mean dataset_2: ',v
w=str(v)
f.write('Mean dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.mean(dataset_3)
print 'Mean dataset_3: ',v
w=str(v)
f.write('Mean dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=scipy.var(dataset_1)
print 'Var dataset_1: ',v
w=str(v)
f.write('Var dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.var(dataset_2)
print 'Var dataset_2: ',v
w=str(v)
f.write('Var dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.var(dataset_3)
print 'Var dataset_3: ',v
w=str(v)
f.write('Var dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=scipy.stats.skew(dataset_1)
print 'sesgo dataset_1: ',v
w=str(v)
f.write('sesgo dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.stats.skew(dataset_2)
print 'sesgo dataset_2: ',v
w=str(v)
f.write('sesgo dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.stats.skew(dataset_3)
print 'sesgo dataset_3: ',v
w=str(v)
f.write('sesgo dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=scipy.stats.kurtosis(dataset_1)
print 'curtosis dataset_1: ',v
w=str(v)
f.write('curtosis dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.stats.kurtosis(dataset_2)
print 'curtosis dataset_2: ',v
w=str(v)
f.write('curtosis dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.stats.kurtosis(dataset_3)
print 'curtosis dataset_3: ',v
w=str(v)
f.write('curtosis dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=kstest(dataset_1,'norm')
print 'KS test, Gaussian dataset_1?',v
w=str(v)
f.write('KS test, Gaussian dataset_1? ')
f.write(w)
f.write("\n")
v=kstest(dataset_2,'norm')
print 'KS test, Gaussian dataset_2?',v
w=str(v)
f.write('KS test, Gaussian dataset_2? ')
f.write(w)
f.write("\n")
v=kstest(dataset_3,'norm')
print 'KS test, Gaussian dataset_3?',v
w=str(v)
f.write('KS test, Gaussian dataset_3? ')
f.write(w)
f.write("\n")
f.write("\n")
f.close()
raw_input()
********************************* *****************************
********************************* ***************************
Los estadísticos que describen un conjunto de datos pueden calcularse de manera sencilla en python.
El análisis de varianza para hacer comparaciones entre las varianzas de varios conjuntos de datos para saber si provienen de poblaciones independientes, se puede hacer con python de manera rápida.
Una vez que se corren algunos ejercicios en python se puede experimentar con programas más complicados.
Visita la página web de python. Ahí puedes descargar python 2.7, por ahora la versión más reciente.
También puedes visitar la página web de SciPy, donde puedes descargar librerías: NumPy, SciPy, SymPy, MatPlotLib y Pandas.
Bibliografía.
Montgomery, Douglas C., and George C. Runger. 2003. Applied statistics and probability for engineers. Third edition. John Willey $ Sons Inc. United States of America.
Cárdenas Montes, Miguel. Estadística. Site: http://wwwae.ciemat.es/~cardenas/curso_MD/Estadistica.pdf
************************************ ******************************
************************************ ******************************
Código Programa1:
# Practica: Estadistica inferencia
# Se trabaja sobre los mismos datos que Estadistica basica
# Prueba de Kruskal-Wallis
# Prueba de Wilcoxon con signo
import scipy.stats
dataset_1=[326.4,324.9,316.3,302.8,317.0,325.4,311.9,322.4,312.1,322.2]
dataset_2=[299.0,301.9,309.4,316.9,304.8,314.2,305.3,308.9,312.5,308.1]
dataset_3=[264.8,275.9,259.0,270.6,266.7,261.8,266.1,268.4,266.2,267.4]
print 'dataset_2: ',dataset_2,'\n','Media: ',scipy.mean(dataset_2)
print 'dataset_3: ',dataset_3,'\n','Media: ',scipy.mean(dataset_3)
f=open('E:/Estadistica_Inferencia.txt','a')
f.write("Dataset_1: " + str(dataset_1) + '\n')
f.write("Media dataset_1: " + str(scipy.mean(dataset_1)) + '\n')
f.write("Dataset_2: " + str(dataset_2) + '\n')
f.write("Media dataset_2: " + str(scipy.mean(dataset_2)) + '\n')
f.write("Dataset_3: " + str(dataset_3) + '\n')
f.write("Media dataset_3: " + str(scipy.mean(dataset_3)) + '\n')
print 'dataset_1 Median: ',scipy.median(dataset_1)
f.write("Dataset_1 Median: " + str(scipy.median(dataset_1)) + '\n')
print 'dataset_2 Median: ',scipy.median(dataset_2)
f.write("Dataset_2 Median: " + str(scipy.median(dataset_2)) + '\n')
print 'dataset_3 Median: ',scipy.median(dataset_3)
f.write("Dataset_3 Median: " + str(scipy.median(dataset_3)) + '\n')
print 'dataset_1 Min: ',min(dataset_1)
f.write("Dataset_1 Min: " + str(min(dataset_1)) + '\n')
print 'dataset_2 Min: ',min(dataset_2)
f.write("Dataset_2 Min: " + str(min(dataset_2)) + '\n')
print 'dataset_3 Min: ',min(dataset_3)
f.write("Dataset_3 Min: " + str(min(dataset_3)) + '\n')
print 'dataset_1 Max: ',max(dataset_1)
f.write("Dataset_1 Max: " + str(max(dataset_1)) + '\n')
print 'dataset_2 Max: ',max(dataset_2)
f.write("Dataset_2 Max: " + str(max(dataset_2)) + '\n')
print 'dataset_3 Max: ',max(dataset_3)
f.write("Dataset_3 Max: " + str(max(dataset_3)) + '\n')
print 'dataset_1 Var: ',scipy.var(dataset_1)
f.write("Dataset_1 Var: " + str(scipy.var(dataset_1)) + '\n')
print 'dataset_2 Var: ',scipy.var(dataset_2)
f.write("Dataset_2 Var: " + str(scipy.var(dataset_2)) + '\n')
print 'dataset_3 Var: ',scipy.var(dataset_3)
f.write("Dataset_3 Var: " + str(scipy.var(dataset_3)) + '\n')
print 'dataset_1 Sesgo: ',scipy.stats.skew(dataset_1)
f.write("Dataset_1 Sesgo: " + str(scipy.stats.skew(dataset_1)) + '\n')
print 'dataset_2 Sesgo: ',scipy.stats.skew(dataset_2)
f.write("Dataset_2 Sesgo: " + str(scipy.stats.skew(dataset_2)) + '\n')
print 'dataset_3 Sesgo: ',scipy.stats.skew(dataset_3)
f.write("Dataset_3 Sesgo: " + str(scipy.stats.skew(dataset_3)) + '\n')
print 'dataset_1 Kurtosis: ',scipy.stats.kurtosis(dataset_1)
f.write("Dataset_1 Kurtosis: " + str(scipy.stats.kurtosis(dataset_1)) + '\n')
print 'dataset_2 Kurtosis: ',scipy.stats.kurtosis(dataset_2)
f.write("Dataset_2 Kurtosis: " + str(scipy.stats.kurtosis(dataset_2)) + '\n')
print 'dataset_3 Kurtosis: ',scipy.stats.kurtosis(dataset_3)
f.write("Dataset_3 Kurtosis: " + str(scipy.stats.kurtosis(dataset_3)) + '\n')
KW_test=scipy.stats.kruskal(scipy.array(dataset_1),scipy.array(dataset_2),scipy.array(dataset_3))
Wi_test_1vs2=scipy.stats.wilcoxon(dataset_1,dataset_2)
Wi_test_2vs3=scipy.stats.wilcoxon(dataset_2,dataset_3)
print 'Kruskal-Wallis test: ',KW_test
f.write("Kruskal-Wallis test: " + str(KW_test) + '\n')
f.write("Wilcoxon signed-rank test dataset_1 vs dataset_2: " + str(Wi_test_1vs2) + '\n')
f.write("Wilcoxon signed-rank test dataset_2 vs dataset_3: " + str(Wi_test_2vs3) + '\n')
print 'Wilcoxon signed-rank test dataset_1 vs dataset_2: ',Wi_test_1vs2
print 'Wilcoxon signed-rank test dataset_2 vs dataset_3: ',Wi_test_2vs3
f.write('\n')
f.close()
raw_input()
******************************* ****************************
Código Programa2:
# Practica: ANOVA
#
# print 'X= %5.3f' % X[i]
import numpy as np
import scipy.stats
import random
from numpy import array
from scipy.stats import kstest
dataset_1=[326.4,324.9,316.3,302.8,317.0,325.4,311.9,322.4,312.1,322.2]
dataset_2=[299.0,301.9,309.4,316.9,304.8,314.2,305.3,308.9,312.5,308.1]
dataset_3=[264.8,275.9,259.0,270.6,266.7,261.8,266.1,268.4,266.2,267.4]
f=open('E:/Estadistica_ANOVA.txt','a')
anova_ans=scipy.stats.f_oneway(dataset_1,dataset_2,dataset_3)
print 'ANOVA: ',anova_ans
f.write('ANOVA: ')
w=str(anova_ans)
f.write(w)
f.write("\n")
# ***
f.write('dataset_1: ')
v=str(dataset_1)
f.write(v)
f.write("\n")
f.write('dataset_2: ')
v=str(dataset_2)
f.write(v)
f.write("\n")
f.write('dataset_3: ')
v=str(dataset_3)
f.write(v)
f.write("\n")
# ***
v=scipy.mean(dataset_1)
print 'Mean dataset_1: ',v
w=str(v)
f.write('Mean dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.mean(dataset_2)
print 'Mean dataset_2: ',v
w=str(v)
f.write('Mean dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.mean(dataset_3)
print 'Mean dataset_3: ',v
w=str(v)
f.write('Mean dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=scipy.var(dataset_1)
print 'Var dataset_1: ',v
w=str(v)
f.write('Var dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.var(dataset_2)
print 'Var dataset_2: ',v
w=str(v)
f.write('Var dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.var(dataset_3)
print 'Var dataset_3: ',v
w=str(v)
f.write('Var dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=scipy.stats.skew(dataset_1)
print 'sesgo dataset_1: ',v
w=str(v)
f.write('sesgo dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.stats.skew(dataset_2)
print 'sesgo dataset_2: ',v
w=str(v)
f.write('sesgo dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.stats.skew(dataset_3)
print 'sesgo dataset_3: ',v
w=str(v)
f.write('sesgo dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=scipy.stats.kurtosis(dataset_1)
print 'curtosis dataset_1: ',v
w=str(v)
f.write('curtosis dataset_1: ')
f.write(w)
f.write("\n")
v=scipy.stats.kurtosis(dataset_2)
print 'curtosis dataset_2: ',v
w=str(v)
f.write('curtosis dataset_2: ')
f.write(w)
f.write("\n")
v=scipy.stats.kurtosis(dataset_3)
print 'curtosis dataset_3: ',v
w=str(v)
f.write('curtosis dataset_3: ')
f.write(w)
f.write("\n")
# ***
v=kstest(dataset_1,'norm')
print 'KS test, Gaussian dataset_1?',v
w=str(v)
f.write('KS test, Gaussian dataset_1? ')
f.write(w)
f.write("\n")
v=kstest(dataset_2,'norm')
print 'KS test, Gaussian dataset_2?',v
w=str(v)
f.write('KS test, Gaussian dataset_2? ')
f.write(w)
f.write("\n")
v=kstest(dataset_3,'norm')
print 'KS test, Gaussian dataset_3?',v
w=str(v)
f.write('KS test, Gaussian dataset_3? ')
f.write(w)
f.write("\n")
f.write("\n")
f.close()
raw_input()
********************************* *****************************
Código Programa3:
# Practica: Estadistica Ajuste
#
import numpy
import numpy as np
import scipy.stats
from scipy import stats
a=numpy.random.normal(size=1000)
loc, std=stats.norm.fit(a)
print loc,'\n',std
f=open('E:/Estadistica_Ajuste.txt','a')
f.write(str(loc) + str(std) + '\n')
v=scipy.mean(a)
print 'Mean: ',v
f.write('Mean: ' + str(v) + '\n')
v=scipy.median(a)
print 'Median: ',v
f.write('Median: ' + str(v) + '\n')
v=min(a)
print 'Min: ',v
f.write('Min: ' + str(v) + '\n')
v=max(a)
print 'Max: ',v
f.write('Max: ' + str(v) + '\n')
v=scipy.var(a)
print 'Var: ',v
f.write('Var: ' + str(v) + '\n')
v=scipy.stats.skew(a)
print 'Sesgo: ',v
f.write('Sesgo: ' + str(v) + '\n')
v=scipy.stats.kurtosis(a)
print 'Kurtosis: ',v
f.write('Kurtosis: ' + str(v) + '\n')
v=scipy.stats.scoreatpercentile(a,90)
print 'Percentil 90: ',v
f.write('Percentil 90: ' + str(v) + '\n')
f.write('\n')
f.close()
raw_input()
********************************* ***************************



No hay comentarios:
Publicar un comentario