Biocombustibles. Especies de ciclo corto y especies perennes. Continuación.
Categoría: 2. Ciencia y tecnología.
Esta entrada presenta un ejercicio de programación en lenguaje Visual C++ (Microsoft, VC++) que ejecuta la simulación con el modelo logístico de crecimiento para una población de árboles de la especie Eucalypthus globulus, estudiada en la entrada titulada "Biocombustibles. Especies de ciclo corto y especies perennes", publicada en septiembre de 2014 en este mismo blog.
Los parámetros para este modelo se habían calculado como sigue:
M=374.1
a=73.82
k=0.4315
En aquella ocasión se compararon el modelo logístico y el modelo exponencial de crecimiento para esta población de E. globulus. El gráfico ilustra el comportamiento de ambos modelos:
a
b
Figura 1. Modelo de crecimiento logístico (a) y modelo de crecimiento exponencial (b) de una especie perenne (E. globulus). En ambas se incluye el rendimiento (ton/ha) para una especie de ciclo anual, en este caso, el maíz (Z. mays).
En este ejercicio se ilustra el uso de la librería fstream de VC++ para el manejo de archivos en la modalidad de escritura. La consola despliega una serie de mensajes para interactuar con el usuario y obtener el tiempo de simulación deseado y preguntando si se quiere realizar una nueva simulación. La rutina se ejecuta tantas veces como el usuario quiere y todos los resultados de una misma sesión de guardan en una archivo de salida de tipo datos.txt. Sin embargo, cada vez que se ejecuta nuevamente el programa, los datos anteriores se borran. Por lo tanto, si se desea recuperar de forma permanente esos datos, es necesario copiar en otro archivo o guardar con un nombre diferente (datos1.txt, por ejemplo).
En esta ocasión se graficaron nuevamente los datos, con el siguiente resultado:
Figura 2. Modelo de crecimiento logístico de crecimiento para una especie perenne (E. globulus) construido a partir de los datos generados con el modelo programado en VC++.
// Código para almacenar datos en archivo de texto:
/*
#include <fstream>
ofstream archivo("E:\\ModLogistico.txt");
if (archivo.fail())
{
cerr << "\n\tNo pudo abrir archivo ...\n";
exit(1);
}
archivo << "\nPara t= " << y << " anhos\tg= " << g << "\n";
archivo.close();
//
*/
Se genera un objeto de tipo ofstream al que se dio el nombre de archivo. Como parámetro se proporciona el nombre y la dirección del archivo de salida. A continuación se verifica que el archivo haya sido abierto (con la instrucción archivo.fail()), de lo contrario se envía un mensaje de error a la consola. En seguida se ponen las instrucciones de escritura de datos en el archivo y finalmente se cierra el archivo, con la instrucción archivo.close().
Figura 3. Consola de VC++ desplegando las preguntas para interaccionar con el usuario solicitando que ingrese el tiempo que quiere considerar en la simulación.
El programa está compuesto por dos funciones 1) modeloLogistico(float tiempo, char modo) y 2)
simulacion( ) y el programa principal int main( ). La función simulacion( ) es llamada dentro de la función modeloLogistico(float tiempo, char modo) y esta a su vez es llamada dentro del programa principal int main( ).
simulacion( ) y el programa principal int main( ). La función simulacion( ) es llamada dentro de la función modeloLogistico(float tiempo, char modo) y esta a su vez es llamada dentro del programa principal int main( ).
Tabla 1. Valores obtenidos en la simulación con Microsoft VC++ para el modelo de crecimiento logístico.
t (años)
|
g (ton/ha)
|
0
|
5
|
1
|
7.64271
|
2
|
11.6382
|
3
|
17.6219
|
4
|
26.4576
|
5
|
39.236
|
6
|
57.1711
|
7
|
81.3136
|
8
|
112.047
|
9
|
148.504
|
10
|
188.3
|
11
|
227.984
|
12
|
264.141
|
13
|
294.475
|
14
|
318.212
|
15
|
335.793
|
16
|
348.292
|
17
|
356.922
|
18
|
362.76
|
19
|
366.655
|
20
|
369.23
|
30
|
374.034
|
40
|
374.099
|
50
|
374.1
|
60
|
374.1
|
70
|
374.1
|
Los valores de la simulación de crecimiento toman un comportamiento asintótico a partir de los 50 años, alcanzando un valor máximo de 374 ton/ha. Estos valores se compararon con los obtenidos en una simulación hecha con el paquete Microsoft Excel, obteniéndose los mismos resultados.
Figura 4. Salida de la simulación en un archivo de texto.
En una nueva simulación el programa pregunta al usuario si necesita cambiar los valores cinéticos. El usuario puede cambiar el valor de M, que es el crecimiento máximo asintótico; el valor de k, que es la constante cinética de crecimiento en la fase exponencial; y g(0), que es la biomasa inicial (por default es de 5.0 ton/ha). El programa calcula automáticamente el nuevo valor de a, utilizando el valor de biomasa inicial y el valor de M.
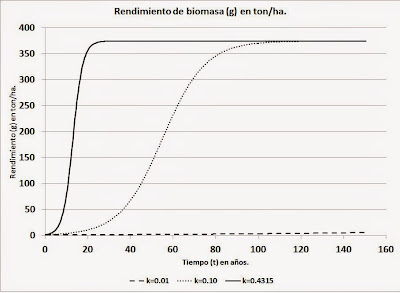
A manera de ejercicio se realizó una serie de simulaciones con tres valores para la constante cinética de crecimiento, k, de 0.01, 0.1 y 0.4315. Los datos se graficaron como se muestra en la figura 5.
Figura 5. Gráficos de las modelaciones para k=0.01, k=0.10 y k=0.4315.
Para obtener un efecto más notorio en el cambio de los valores de k, se utilizó un valor de biomasa inicial g(0)=1.3 ton/ha. De este modo, el crecimiento inicial se retrasa con respecto a la simulación hecha antes, donde se utilizó el valor predefinido g(0)=5.0 ton/ha.
Figura 4. Salida de la simulación en un archivo de texto.
En una nueva simulación el programa pregunta al usuario si necesita cambiar los valores cinéticos. El usuario puede cambiar el valor de M, que es el crecimiento máximo asintótico; el valor de k, que es la constante cinética de crecimiento en la fase exponencial; y g(0), que es la biomasa inicial (por default es de 5.0 ton/ha). El programa calcula automáticamente el nuevo valor de a, utilizando el valor de biomasa inicial y el valor de M.
A manera de ejercicio se realizó una serie de simulaciones con tres valores para la constante cinética de crecimiento, k, de 0.01, 0.1 y 0.4315. Los datos se graficaron como se muestra en la figura 5.
Figura 5. Gráficos de las modelaciones para k=0.01, k=0.10 y k=0.4315.
Para obtener un efecto más notorio en el cambio de los valores de k, se utilizó un valor de biomasa inicial g(0)=1.3 ton/ha. De este modo, el crecimiento inicial se retrasa con respecto a la simulación hecha antes, donde se utilizó el valor predefinido g(0)=5.0 ton/ha.
Conclusiones.
- Almacenar los datos de salida de una simulación numérica en VC++ en un archivo de tipo archivo.txt facilita hacer una ulterior manipulación para su análisis y su presentación gráfica, utilizando paquetes como hojas de cálculo electrónicas (como Microsoft Excel y Lotus 123) o en paquetes matemáticos (como Matlab, Mathworks, Mathematica o Polymath).
- Los valores obtenidos en la simulación en el modelo logístico de crecimiento con Microsoft VC++ son los mismos que se obtuvieron con el paquete Microsoft Excel.
Bibliografía:
S. Pérez; C. J. Renedo; A. Ortiz; M. Mañana; D. Silió; and J Peredo. 2012. Comparison of energy potential of the Eucalyptus globulus and the Eucalyptus nitens. http://www.icrepq.com/icrepq06/285%20Perez.pdf
Malik, M.S; C. Surendran and K. Kailasham. 2003.
A MATHEMATICAL MODEL FOR PREDICTING THE GROWTH OF Eucalyptus globulus UNDER AGROFORESTRY PLANTATION
XII World Forestry COngress, 2003. Québeq City, Canada.
Disponible: http://www.fao.org/docrep/ARTICLE/WFC/XII/1021-B1.HTM
Sitios visitados:
Anexo. Programa para calcular el crecimiento de una población de E. globulus (en ton/ha), mediante un modelo logístico de crecimiento.
#include <iostream>
#include <fstream>
#include <iomanip>
#include <Windows.h>
using namespace std;
float m=374.1;
float a=73.82;
float k=0.4315;
float g_0=5.0;
float t=0;
int tiempo=200;
char modeloDecision() {
char b;
std::cout << "\nDesea realizar nueva simulacion? ... Si (y) No (n) ... \t";
std::cin >> b;
char c='0';
if (b == 'y') {
std::cout << "\nDesea modificar valores cineticos? ... Si (y) No (n) ... \t";
std::cin >> c;
}
else {
std::cout << "\nNo se hara una nueva simulacion ...";
return 0;
}
if (c == 'y') {
std::cout << "\nNuevo valor para M=374.1: ";
std::cin >> m;
std::cout << "\nNuevo valor para k=0.4315: ";
std::cin >> k;
std::cout << "\nNuevo valor para g(0)=5.0 ton/ha: ";
std::cin >> g_0;
a = (m-g_0)/g_0;
std::cout << "\nSe calculo nuevo valor para a= " << a << "\n";
std::cout << "\nAhora introduce la extension para la simulacion t=100 anhos: ";
std::cin >> tiempo;
tiempo *= 2;
t = 0; // Refresca el valor de t.
}
else {
std::cout << "\nNueva simulacion con M=374.1; a=73.82; k=0.4315 ...\n";
}
return b;
}
float modeloLogistico(float b) {
float f=m/(1+(a*exp(-k*b)));
return f;
}
float modeloPunto(float r) {
float w=m/(1+(a*exp(-k*r)));
return w;
}
int main() {
std::cout << "\t\t*** USO DE LA INSTRUCCION Return #; ***" << "\n\n";
char f='0';
ofstream archivo("E:\\Return.txt", ios::app);
do {
if (archivo.fail()) {
cerr << "\n\tNo pudo abrir archivo ...\n";
exit(1);
}
std::cout << "\nIntroduzca el tiempo para la simulacion (anhos, con dos decimales):\t";
float y;
std::cin >> y;
std::cout << "\n********** Nueva simulacion para y= " << y << " anhos *************\n\n";
SYSTEMTIME lt;
GetLocalTime(<);
printf(" The local time is: %02d:%02d:%02d\n", lt.wHour, lt.wMinute, lt.wSecond);
printf(" The local date is: %04d-%02d-%02d\n", lt.wYear, lt.wMonth, lt.wDay);
archivo << "\n********** Nueva simulacion para y= " << y << " anhos *************\n\n";
archivo << setprecision(2);
archivo << "\n" << lt.wHour << ":" << lt.wMinute << ":" << lt.wSecond;
archivo << setprecision(4);
archivo << "\n" << lt.wYear;
archivo << setprecision(2);
archivo << "-" << lt.wMonth << "-" << lt.wDay;
archivo << setiosflags(ios::fixed);
archivo << setiosflags(ios::showpoint);
archivo << setprecision(2);
archivo << "\nValores para la modelacion: \n" << "M= " << m << "\nk= " << k << "\na= " << a << "" << tiempo;
archivo << "\nt_anho" << "\tg_ton/ha\n";
for (int x=0; x<tiempo; x++) {
float g = modeloLogistico(t);
std::cout << "t= " << t << "\tg= " << g << "\n";
archivo << t << "\t" << g << "\n";
t+=0.5;
}
float g = modeloPunto(y);
std::cout << "\nPara t= " << y << " anhos\tg=" << g << "\n";
archivo << "\nPara t= " << y << " anhos\tg= " << g << " ton/ha\n";
f = modeloDecision();
}
while (f == 'y');
archivo.close();
std::cout << "\n\t";
cin.get(); // Espera a que se presione una tecla.
return 0;
}
#include <fstream>
#include <iomanip>
#include <Windows.h>
using namespace std;
float m=374.1;
float a=73.82;
float k=0.4315;
float g_0=5.0;
float t=0;
int tiempo=200;
char modeloDecision() {
char b;
std::cout << "\nDesea realizar nueva simulacion? ... Si (y) No (n) ... \t";
std::cin >> b;
char c='0';
if (b == 'y') {
std::cout << "\nDesea modificar valores cineticos? ... Si (y) No (n) ... \t";
std::cin >> c;
}
else {
std::cout << "\nNo se hara una nueva simulacion ...";
return 0;
}
if (c == 'y') {
std::cout << "\nNuevo valor para M=374.1: ";
std::cin >> m;
std::cout << "\nNuevo valor para k=0.4315: ";
std::cin >> k;
std::cout << "\nNuevo valor para g(0)=5.0 ton/ha: ";
std::cin >> g_0;
a = (m-g_0)/g_0;
std::cout << "\nSe calculo nuevo valor para a= " << a << "\n";
std::cout << "\nAhora introduce la extension para la simulacion t=100 anhos: ";
std::cin >> tiempo;
tiempo *= 2;
t = 0; // Refresca el valor de t.
}
else {
std::cout << "\nNueva simulacion con M=374.1; a=73.82; k=0.4315 ...\n";
}
return b;
}
float modeloLogistico(float b) {
float f=m/(1+(a*exp(-k*b)));
return f;
}
float modeloPunto(float r) {
float w=m/(1+(a*exp(-k*r)));
return w;
}
int main() {
std::cout << "\t\t*** USO DE LA INSTRUCCION Return #; ***" << "\n\n";
char f='0';
ofstream archivo("E:\\Return.txt", ios::app);
do {
if (archivo.fail()) {
cerr << "\n\tNo pudo abrir archivo ...\n";
exit(1);
}
std::cout << "\nIntroduzca el tiempo para la simulacion (anhos, con dos decimales):\t";
float y;
std::cin >> y;
std::cout << "\n********** Nueva simulacion para y= " << y << " anhos *************\n\n";
SYSTEMTIME lt;
GetLocalTime(<);
printf(" The local time is: %02d:%02d:%02d\n", lt.wHour, lt.wMinute, lt.wSecond);
printf(" The local date is: %04d-%02d-%02d\n", lt.wYear, lt.wMonth, lt.wDay);
archivo << "\n********** Nueva simulacion para y= " << y << " anhos *************\n\n";
archivo << setprecision(2);
archivo << "\n" << lt.wHour << ":" << lt.wMinute << ":" << lt.wSecond;
archivo << setprecision(4);
archivo << "\n" << lt.wYear;
archivo << setprecision(2);
archivo << "-" << lt.wMonth << "-" << lt.wDay;
archivo << setiosflags(ios::fixed);
archivo << setiosflags(ios::showpoint);
archivo << setprecision(2);
archivo << "\nValores para la modelacion: \n" << "M= " << m << "\nk= " << k << "\na= " << a << "" << tiempo;
archivo << "\nt_anho" << "\tg_ton/ha\n";
for (int x=0; x<tiempo; x++) {
float g = modeloLogistico(t);
std::cout << "t= " << t << "\tg= " << g << "\n";
archivo << t << "\t" << g << "\n";
t+=0.5;
}
float g = modeloPunto(y);
std::cout << "\nPara t= " << y << " anhos\tg=" << g << "\n";
archivo << "\nPara t= " << y << " anhos\tg= " << g << " ton/ha\n";
f = modeloDecision();
}
while (f == 'y');
archivo.close();
std::cout << "\n\t";
cin.get(); // Espera a que se presione una tecla.
return 0;
}